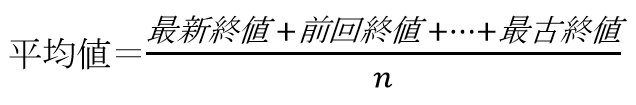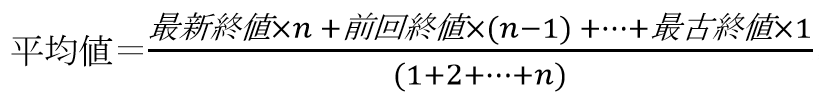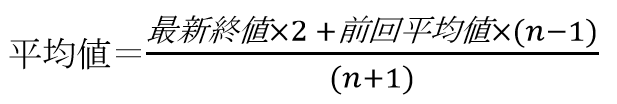本記事ではbitFlyer Lightningで表示できるテクニカルツールの平滑移動平均線について説明します。
移動平均線とは、一定期間の終値の平均をグラフにしたものです。上昇トレンドや下降トレンドを判断するために使ったり、移動平均線を壁のように考えて価格の動きを予想するのに使ったりします。
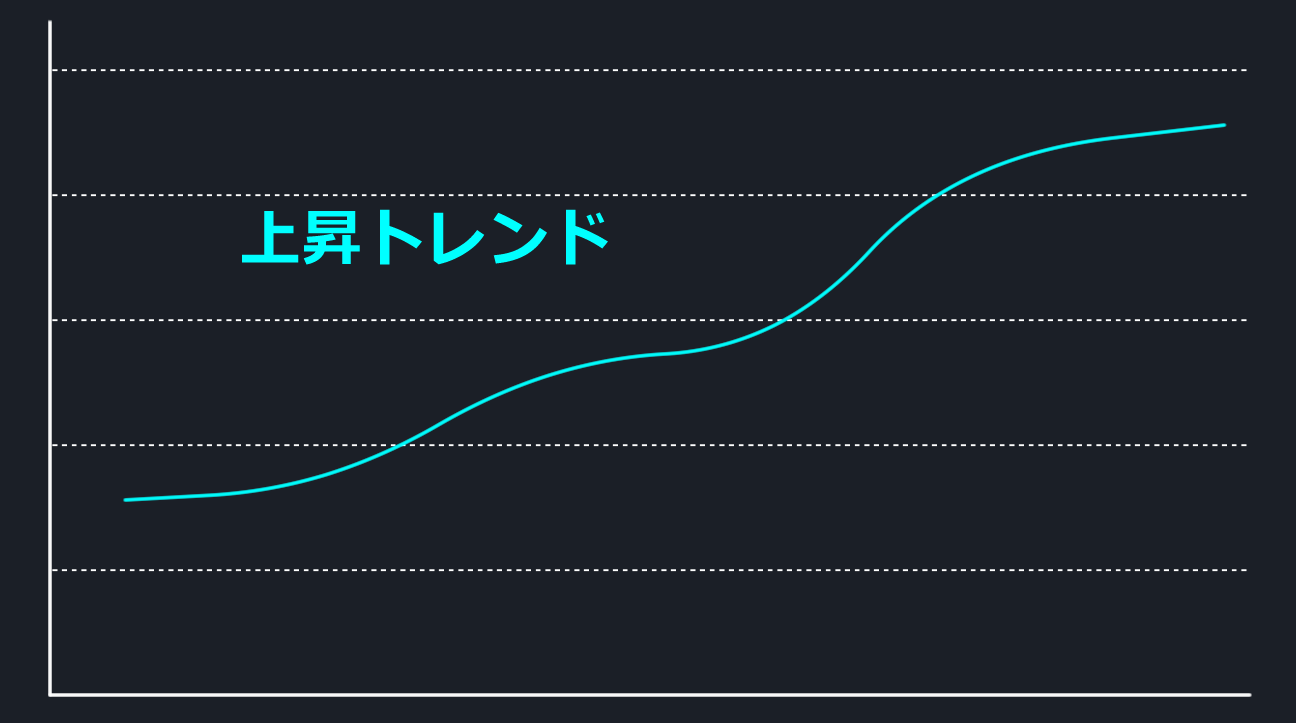
移動平均線が右肩上がりになっているものを上昇トレンドといいます。価格が上がって行っているということです。ビットコインを保有している人がこれを見るとテンションが上がります。
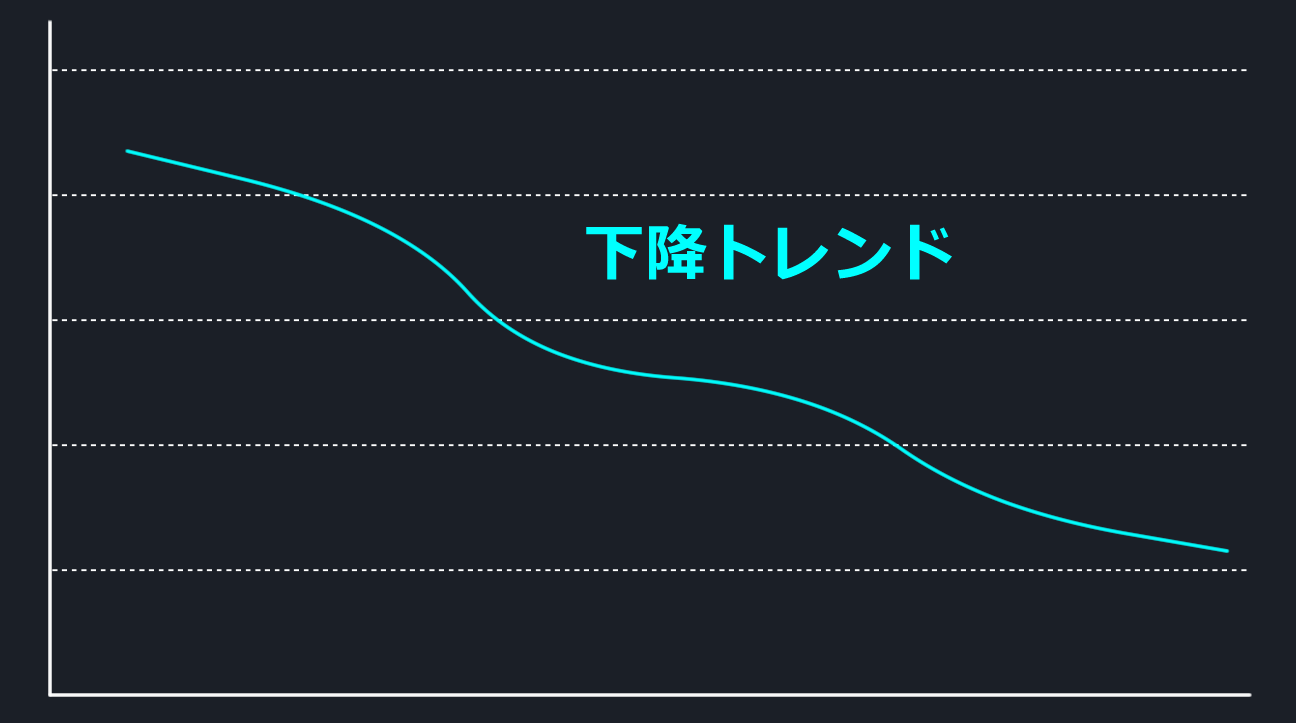
移動平均線が右肩下がりになっているものを下降トレンドといいます。価格が下がって行っているということです。ビットコインを保有している人がこれを見るとテンションが下がります。
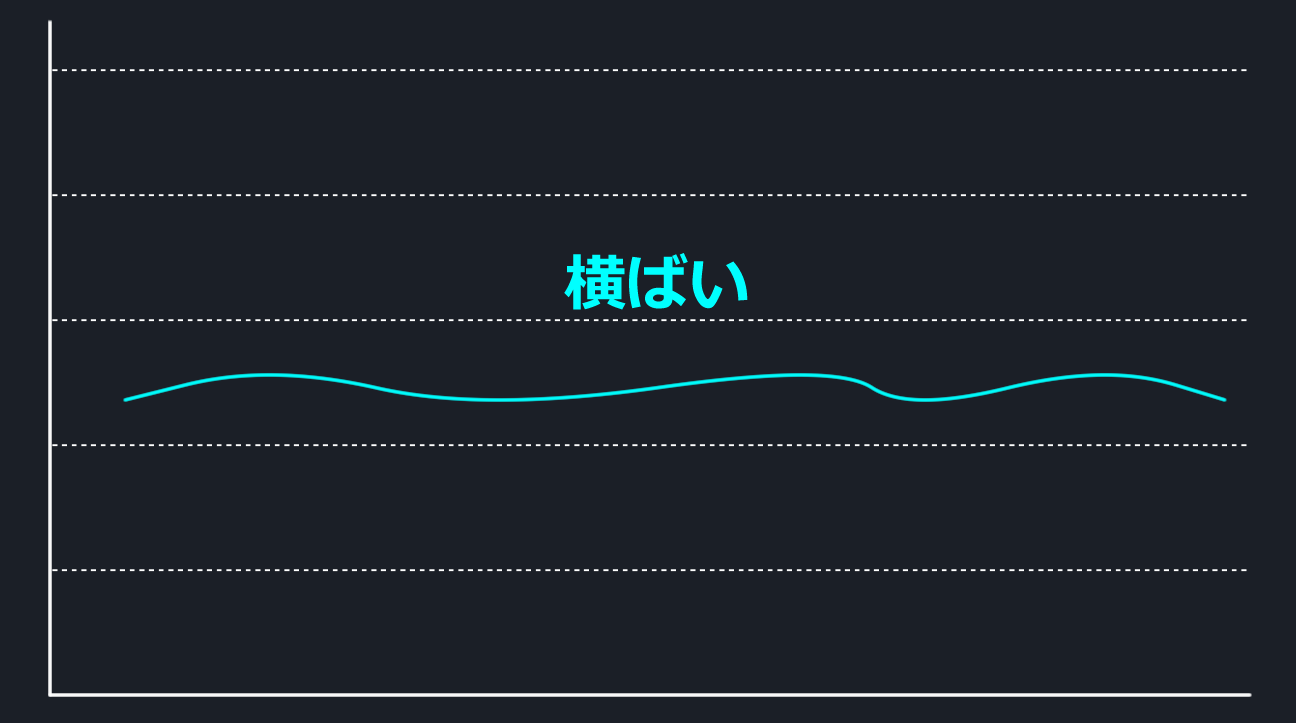
大きな値動きがなく、上がったり下がったりを繰り返してトレンドが定まらないものを「横ばい」と言います。ビットコインを保有している人がこれをみたらムズムズします。
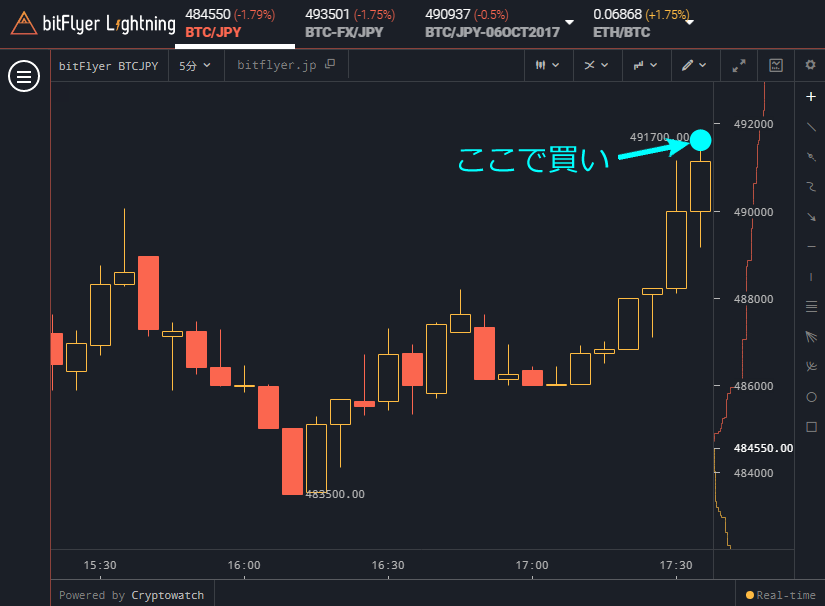
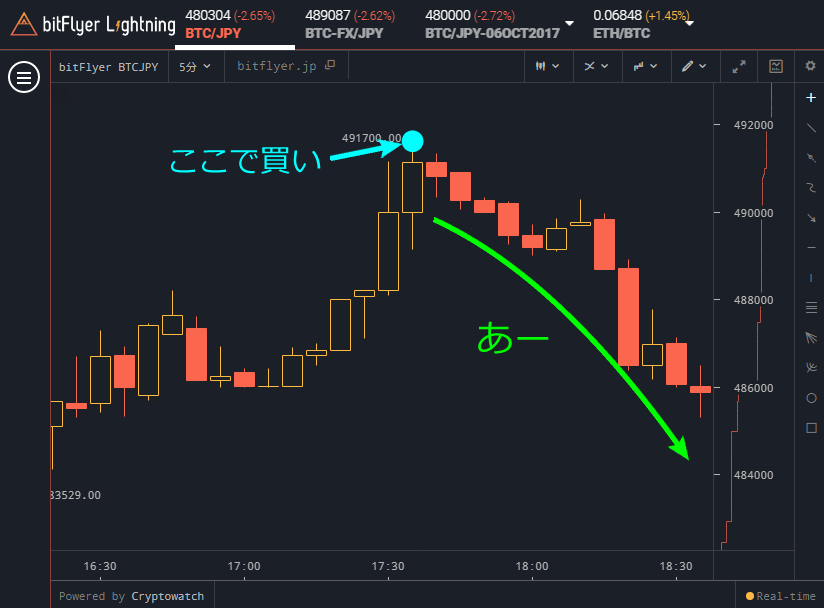
ここで太郎の話を１つ。ビットコインの価格がしばらくジリジリと下がるのが続いたあと、太郎は下図チャートを見て
と思って買いました。
無事買えたと思ったら、価格がまたジリジリと下がり始めました。
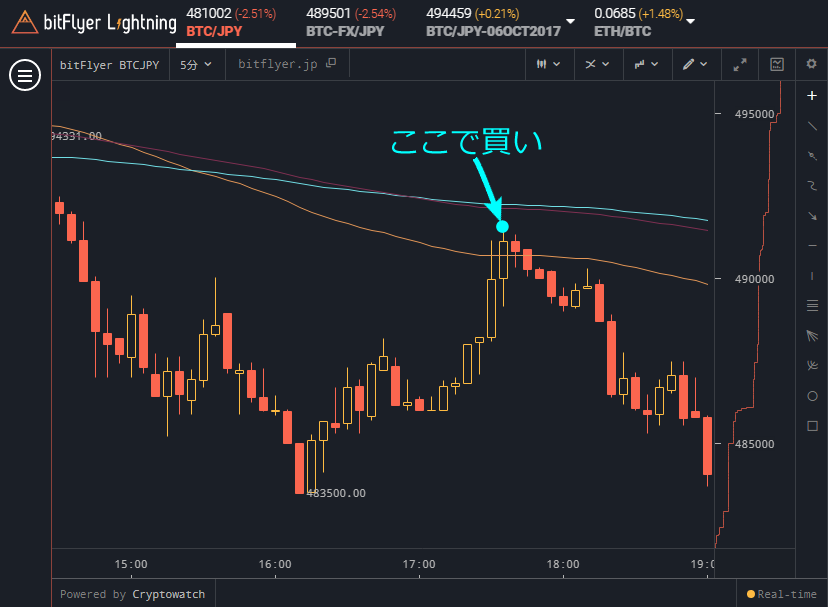
移動平均線を引いてみると、下降トレンドが続いていたことが分かりました。太郎は
と思いながら損切りしました。確かに、まだ下降トレンドであることが把握できていたら買うのを控えていたかも知れません。移動平均線が教えてくれるトレンドは、買売タイミングを考える上での参考になるのでかなり多くのトレーダーが利用しています。
bitFlyer Lightningで使われている移動平均線は「指数平滑移動平均線」と呼ばれるものです。有名な移動平均線に「単純移動平均線」と「加重移動平均線」がありますが、まずはそれぞれの移動平均線の作り方と違いを見てみましょう。
単純移動平均線
単純移動平均線はその名の通り単純です。集計対象の個数をnとして以下の計算式で平均値を計算します。
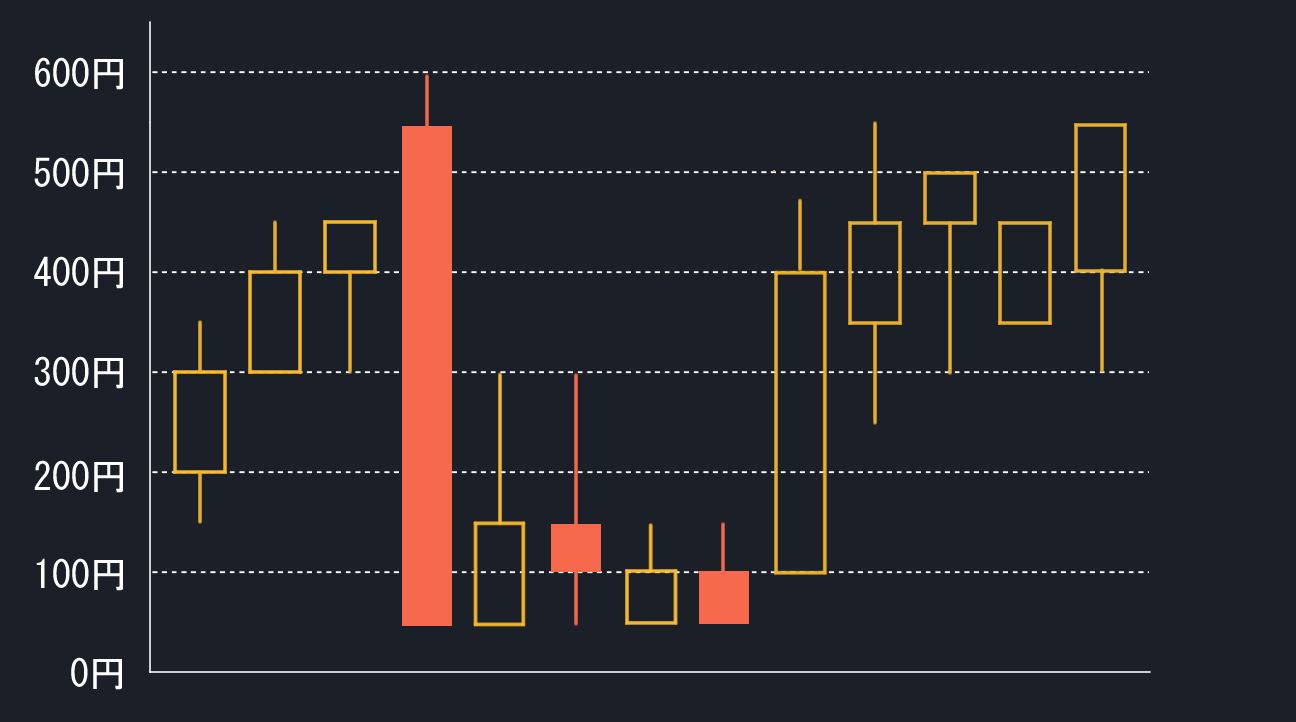
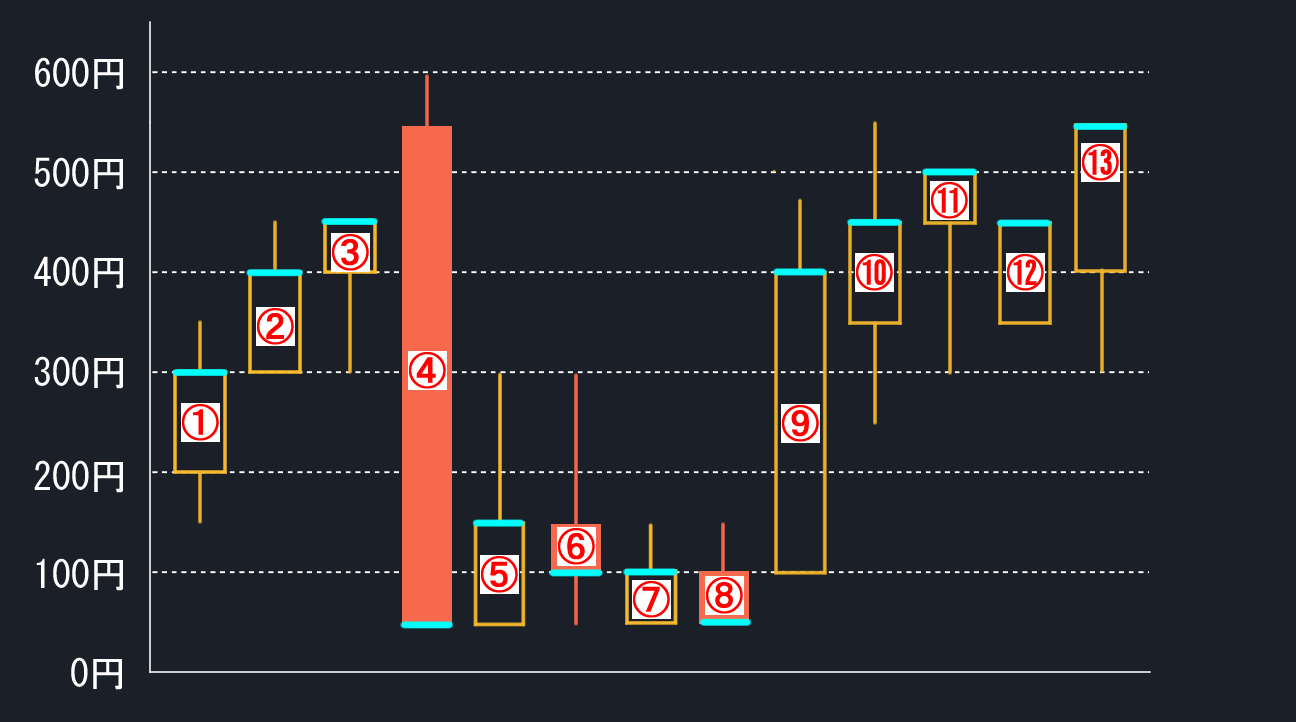
何だか式を見てもピンとこないので実際に単純移動平均線を作ってみましょう。下図のロウソク足のチャートに書き込みます。
分かりやすいように、各ローソクに番号と終値の印（水色線）を付けました。集計範囲は直近5個とします。
⑤のローソク足から始めます。
（手順１）さかのぼって5個ぶんのローソク足の終値を合計します。①300円＋②400円＋③450円＋④50円＋⑤150円＝1350円
（手順２）合計値を終値の個数で割ります。1350円÷5個＝270円
（手順３）⑤の列のY座標の270円に点を付けます。
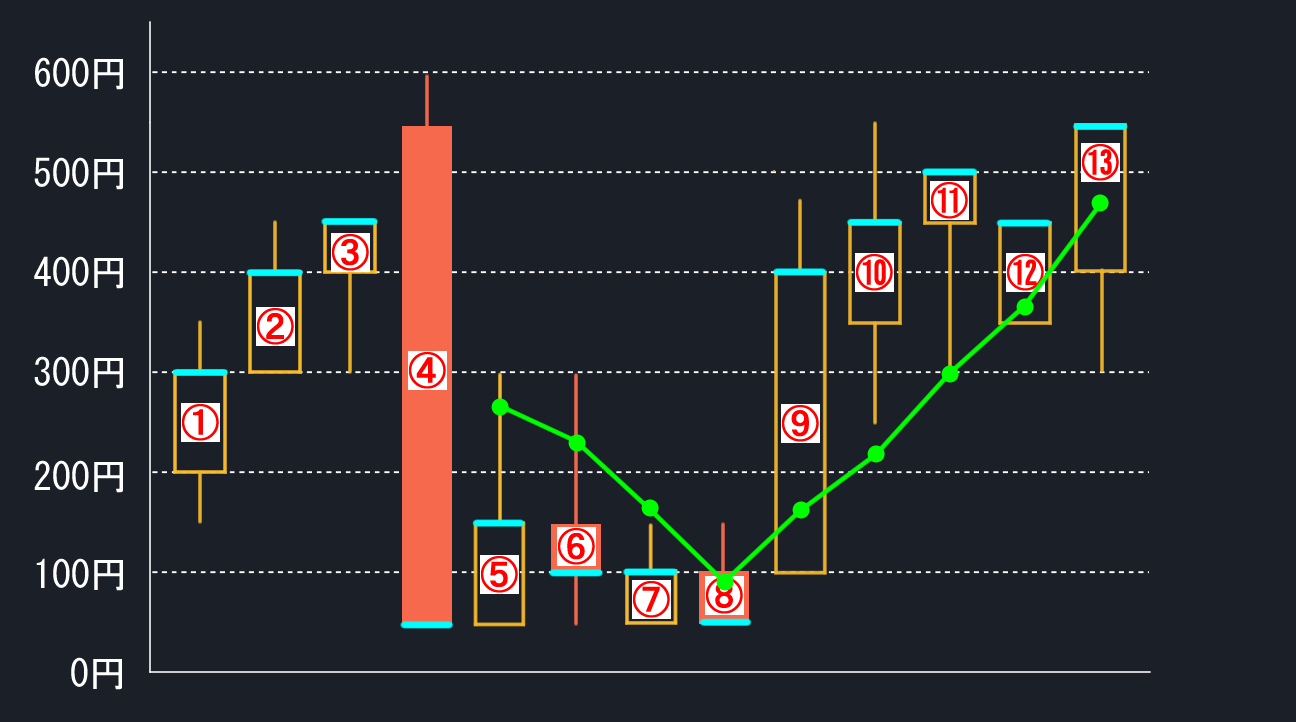
上記手順を⑥から⑬で繰り返し、最後に点を結んで完成です。完成した単純移動平均線は下図になります。
単純移動平均線は分かりやすくていいのですが問題があります。
1つ目の問題は、集計対象の終値をすべて平等に扱っている点です。最新の終値でも大分昔の終値でも集計対象から外れるまでは平均値に与える影響力はどれも同じということです。短期的な大きな値動きは時間と共に徐々に平均値への影響力が薄れていってもらいたいですね。
2つ目の問題は、集計対象から外れている終値を完全に無視する点です。例えば、先ほどの例の⑫の平均値は価格が低い⑧の終値を含んだ平均ですが、⑬になったとたんに価格が低かったころを完全に忘れた直近5個ぶんの平均になっています。
加重移動平均線
単純移動平均線の「集計対象の終値をすべて平等に扱っている」の欠点を解消している平均線に加重移動平均線があります。
集計対象の個数をnとして以下の計算式で平均値を計算します。
新しい終値ほど平均値への影響が大きく、古い終値ほど平均値への影響が小さくなるのがイメージできるでしょうか。なんだかややこしいので、先ほどのチャートに加重移動平均線を書き込んでみましょう。集計範囲は直近5個とします。
⑤のローソク足から始めます。
最新の終値150円に5を掛ける。前回の終値50円に4を掛ける。前々回の終値450円に3を掛ける。前々々回の終値400円に2を掛ける。前々々々回の終値300円に1を掛ける。それを全部足して15（＝1+2+3+4+5）で割ります。
平均値＝（150×5 + 50×4 + 450×3 + 400×2 + 300×1）÷（1+2+3+4+5）＝ 226.6円
⑤の列のY座標に226.6円の点を付けます。上記手順を⑥から⑬まで繰り返します。
加重することで15個の値の平均をとるのと同じことになったからです。
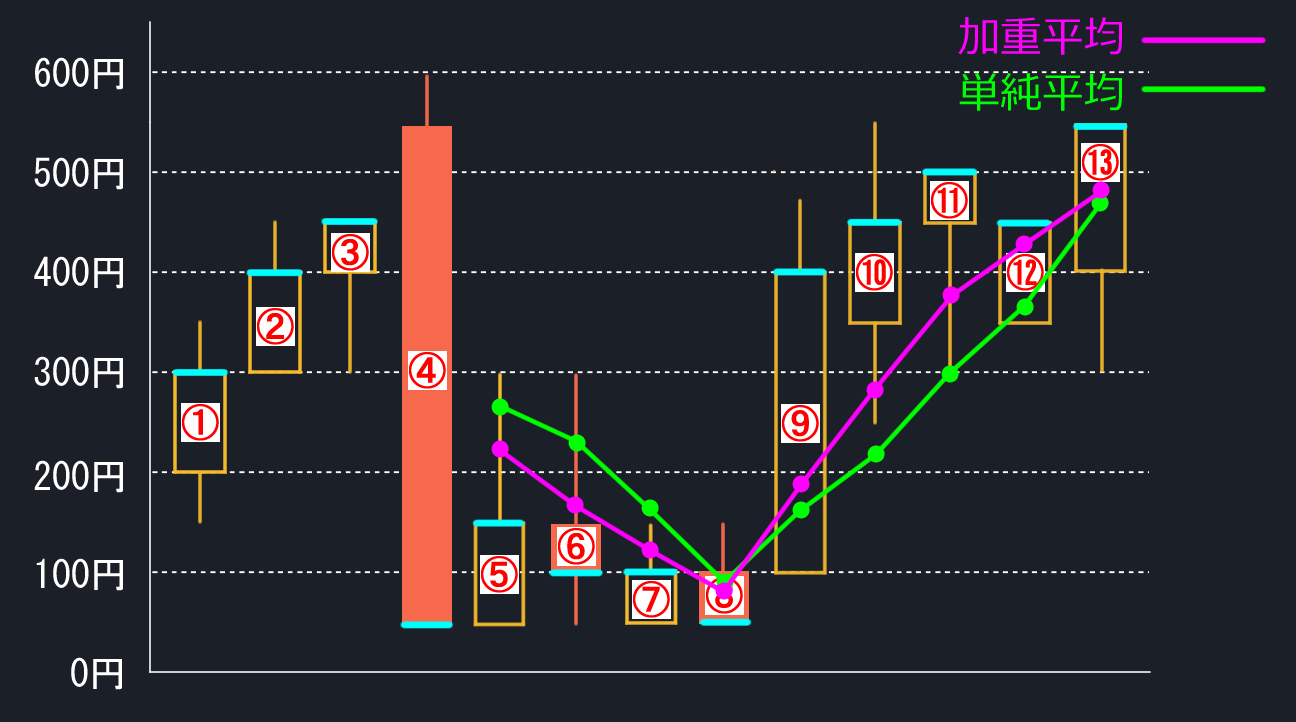
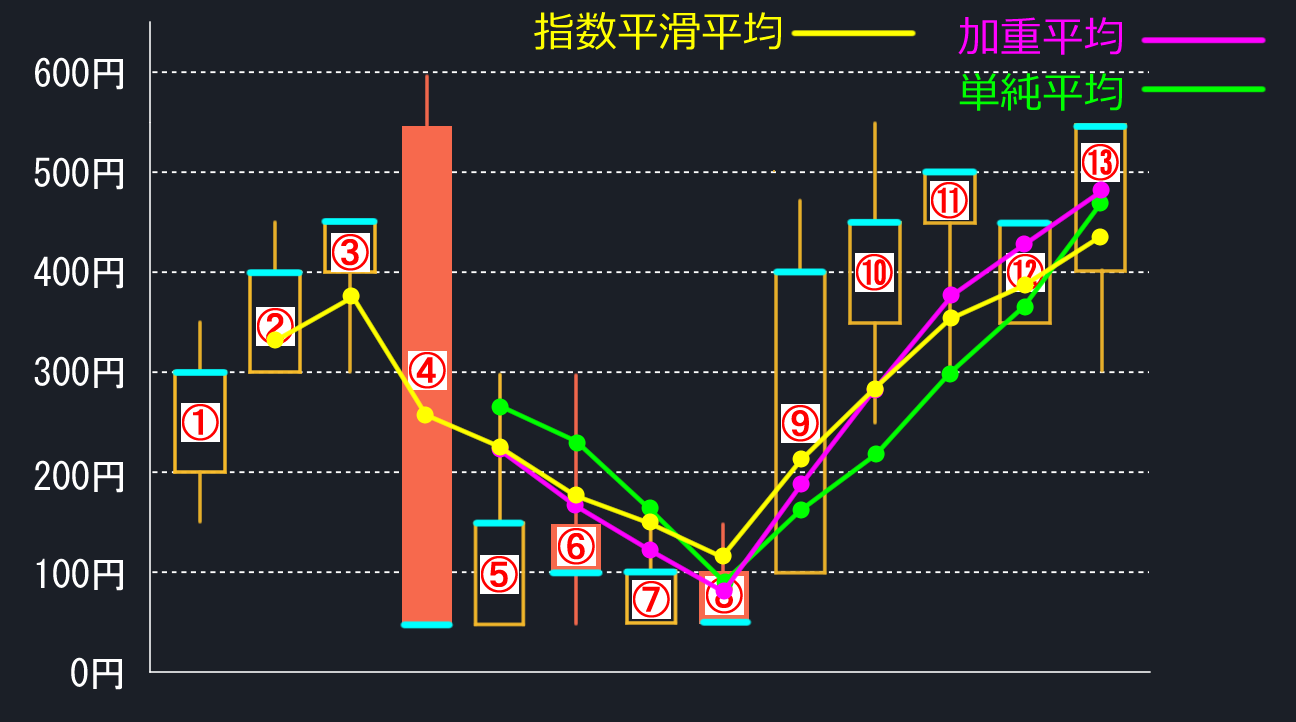
下図が結果です。単純平均より加重平均のほうが最新終値に近いグラフになっていることが分かります。
指数平滑移動平均線
単純移動平均線と加重移動平均線には「集計対象から外れている終値を完全に無視する」という欠点があります。その欠点を解消している平均線に「指数平滑移動平均線」があります。
集計対象の個数をnとして以下の計算式で平均値を計算します。
最新の終値を2倍にして平均値への影響を大きくしているのと、過去の終値には過去の平均値を利用することで集計対象を越えたすべての終値の影響を受けている数値にしています。
これまたややこしいので、先ほどチャートに指数平滑移動平均線を書き込んでみましょう。集計範囲は5個とします。
②のローソク足から始めます。
最新の終値400に2を掛けます。①の終値300を前回平均値として4を掛けます。この2つを足して6で割ります。
平均値＝（400×2+300×4）÷6 ＝333.3
②の列のY座標に333.3円の点を付けます。
終値6個ぶんを足したからです。最新終値は平均値への影響を大きくするために2個ぶんカウントしています。
完成した指数平滑移動平均線は下図になります。対象範囲が短いので違いがあまり出ていませんが、⑬を見ると、指数平滑移動平均は加重平均や単純平均よりも低くなっています。すなわち⑧より昔の低価格の影響を受けていることが分かります。
指数平滑移動平均線を表示する
bitFlyer Lightningの指数平滑移動平均線を見てみましょう。といっても、実は指数平滑移動平均線は最初からチャートに表示されています。
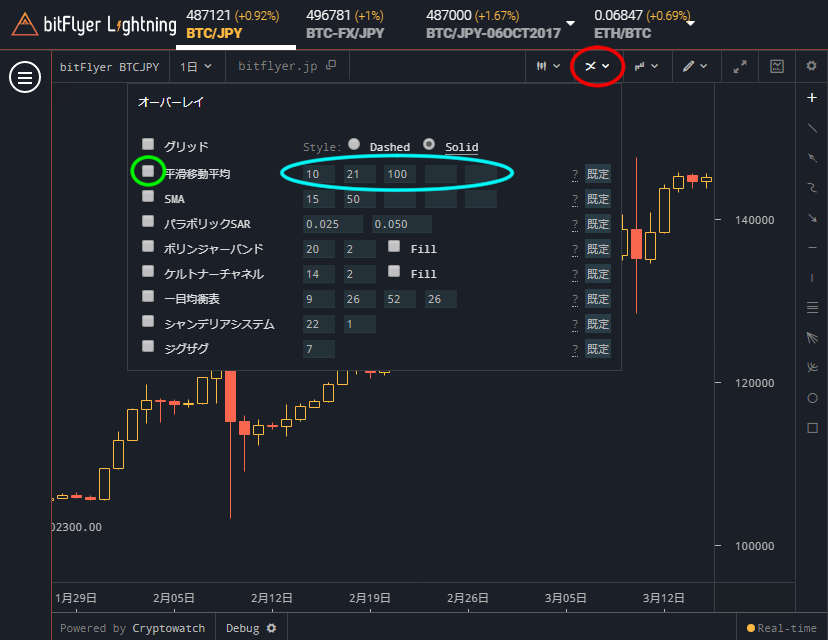
表示、非表示を切り替えるには下図赤枠にマウスポインタを合わせます。すると下にオーバーレイの設定項目が表示されるので、平滑移動平均のチェックを外せば非表示になり、チェックを入れれば表示されます。
平滑移動平均の右に表示されている5つの入力欄（下図水色枠）は集計範囲を設定する箇所で、最初は10、21、100が設定されています。つまり、3本の指数平滑移動平均線が表示されるということです。5つの入力欄をすべて埋めれば5本表示できます。
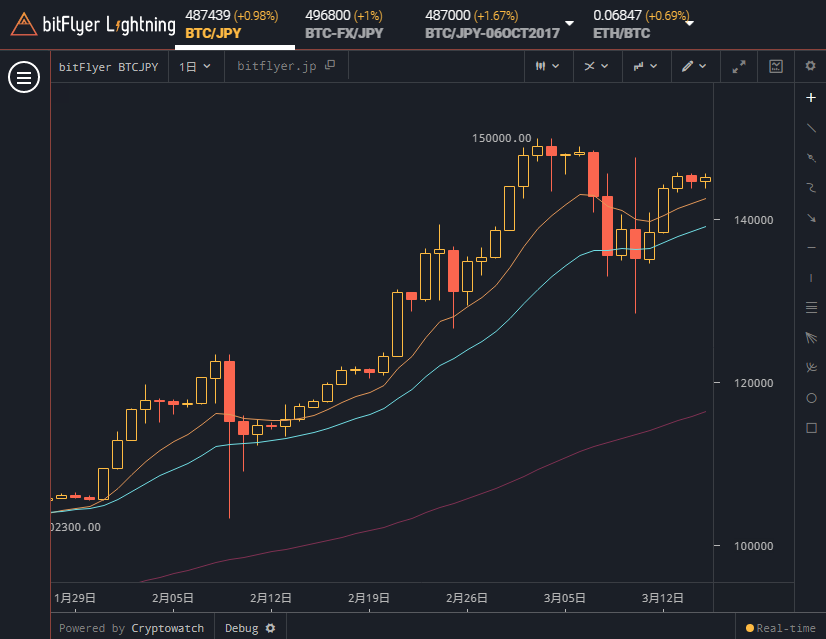
下図が指数平滑移動平均線を表示した結果です。色の違う3本の線が表示されています。気持ちいい上昇トレンドですね。指数平滑移動平均線を利用した売買タイミングの考え方については今後の記事で説明します。
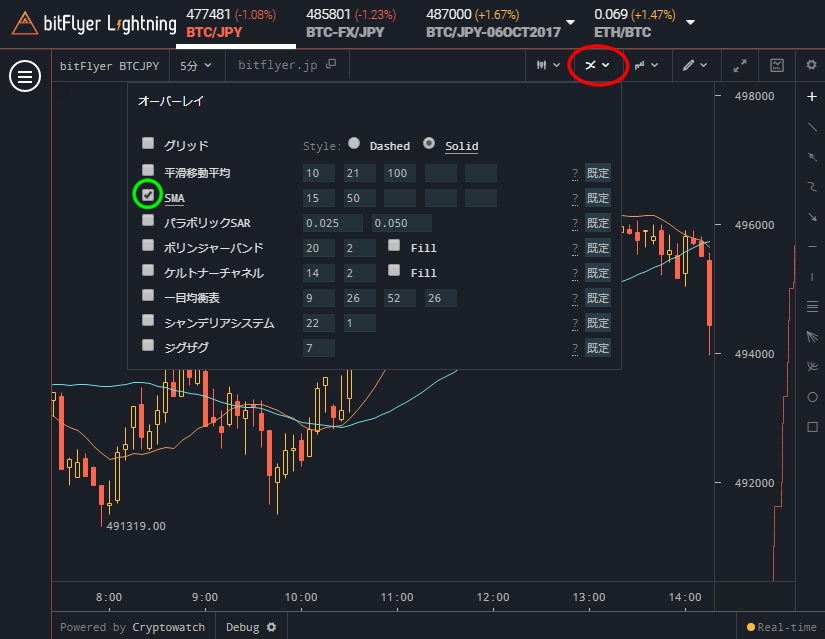
単純移動平均線を表示する
bitFlyer Lightningでは単純移動平均線も表示することができます。下図赤枠にマウスポインタを合わせると下にオーバーレイの設定項目が表示されます。SMAが単純移動平均線（Simple Moving Average）の略で、チェックを入れると表示できます。5本まで表示できるのは平滑移動平均と同じです。
細かいですが、1つ気になったのはオーバーレイの設定項目の指数平滑移動平均は日本語表記（平滑移動平均）で、単純移動平均は英語略記（SMA）であることです。英語か日本語かどちらかに統一して欲しいですね。（2017年10月4日）
[tp_table id=9 /]
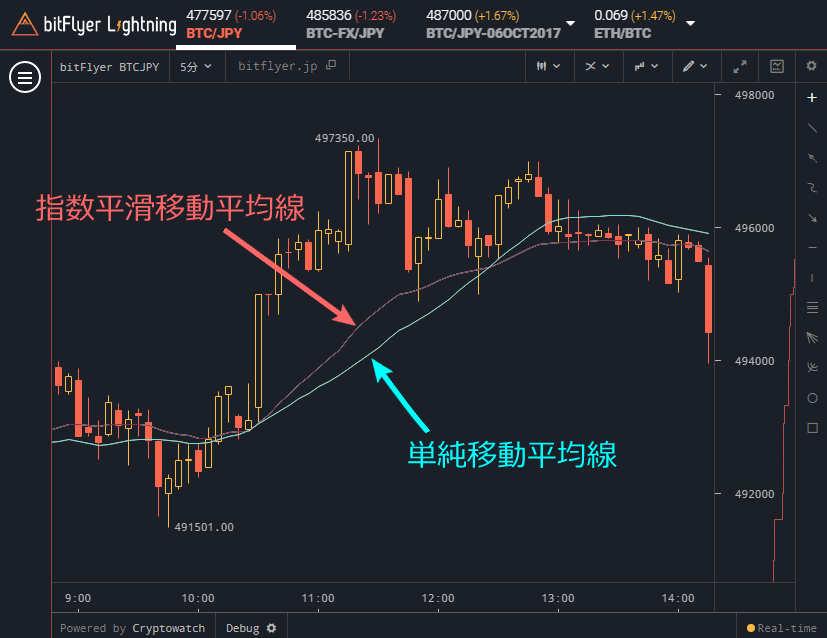
下図は指数平滑移動平均線と単純移動平均線を同じ集計個数（30個）で表示したものです。グラフを見て分かるように、指数平滑移動平均線は単純移動平均線よりトレンドの切替わりへの反応が早いです。なぜなら、直近の終値の影響力を大きくしているからです。
[exchange]
コメント一覧 （6件）
質問です
私は単純移動平均線を使いたいのですが、平均線の資料になる足の数はどうやって決めればいいですか？（1時間、4時間、1日足のチャートをよく見ます）
それと、この説明に使われている画像のようにCryptowatchでローソク足をLightChartの色（オレンジ、黄色）にするにはどう設定すればいいですか？
あともう一つ、投稿画像のように、PCだとチャート画面を拡大しても横にだけ拡大されて見にくくなるのですが、どうすればいいでしょうか？（PCの画面設定の拡大縮小を使ってもダメでした）（タブレットやスマホでは普通です）
長文失礼しました。
平均線の足の決め方はこうでなきゃならないというのは無かったと思います。
それぞれ、自分のトレードスタイルや検証結果、経験をもとに好みのローソク足、移動平均線を使っているのだと思ってます。
あとは、一番見ている人が多い設定にしたほうが相場の動きを読みやすくなると言われているので、その辺りを考慮にいれて決めるのがいいと思います。
私が設定の仕方を知らないだけかも知れませんが、Cryptowatchのローソク足の色は変更できないと思います。この記事のCryptowatchの表示は昔のもので、そのころは色がマッチしていい感じだったのですが、ある日突然表示が変わりました。
チャートの拡大については、私はチャートを拡大したあと、マウスホイールでズームイン、ズームアウトさせて見ていて、特に見づらいと感じないのですがそういうことではなくてですか？
分かりました、では移動平均線はいろいろ試してみます。
そうなんですね、昔はその色でなぜか色変わったんですね…
はい、私もマウスホイールで拡大すると管理人さんの画像のように波形がしっかりでてくるのではなく、先ほど投稿した画像のようにローソク足が横に太くなって上下から潰されたような形になります（縦横比が変わってる？）
ただ、LightChartやCryptowatchの本サイトでは特に問題なく見られます
なので今はCryptowatchの本サイトで分析してます
ありがとうございました
不思議な現象ですね。
ブラウザを変えても同じ症状がでるのでしょうか？
パソコンではブラウザはいつもMicrosoft Edgeを使ってます。
しかし、先ほどChromeで見てみると違和感ない画面で見られました。
そういえばスマホやタブレットではいつもChromeを使ってるので恐らくMEに問題があったのだと思います。
これからはChromeでチャートを見るようにします。ありがとうございました。
スクロールが上手くできるようになって良かったですね。
私のPCのEdgeで試してみたところ、問題なくスクロールできました。
Edgeのキャッシュをクリアすると改善されるかも知れないので、時間があるときにでも試してみて下さい。