bitFlyer Lightning ボリンジャーバンドの見方
本記事ではbitFlyer Lightningで使えるボリンジャーバンドについて説明します。
ボリンジャーバンドとは、移動平均線と、移動平均線に対する価格のばらつきを想定した上下の補助線のことです。移動平均線って何だという人は次の記事を参考にして下さい。
⇒「移動平均線とは」
「価格のばらつきを想定した上下の補助線」は標準偏差というものを利用して引かれています。標準偏差の詳しい説明については他の専門サイトや教科書に譲るとして、本記事では簡単なイメージを説明します。
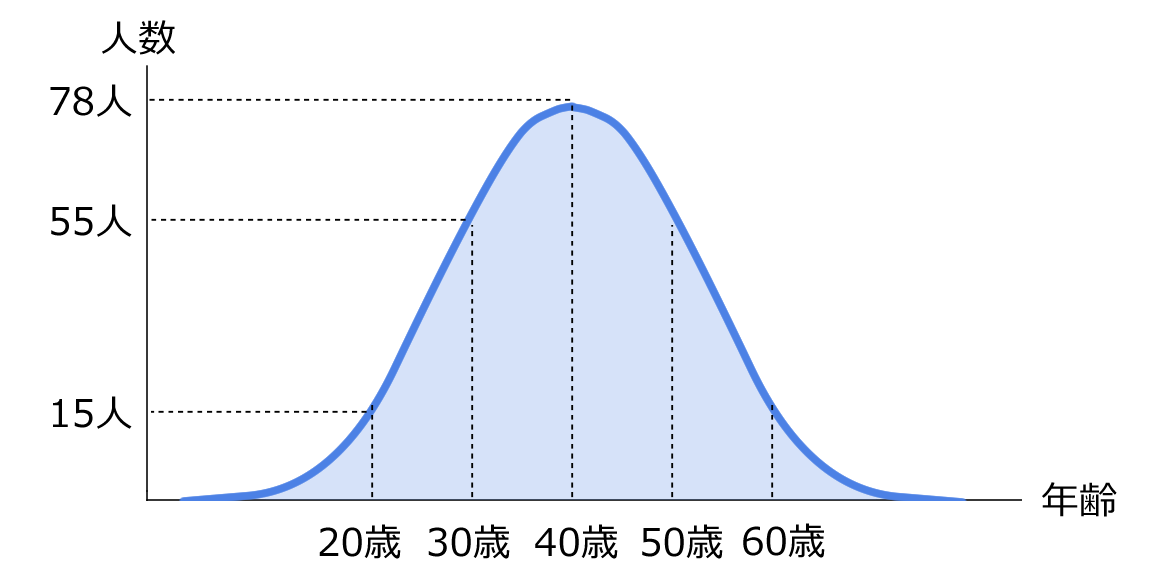
例えば、あるグループ会員の年齢と人数が下図のような釣り鐘のような分布になっていたとします。40歳が一番多く、40歳から離れるにつれ人数が少なくなっています。
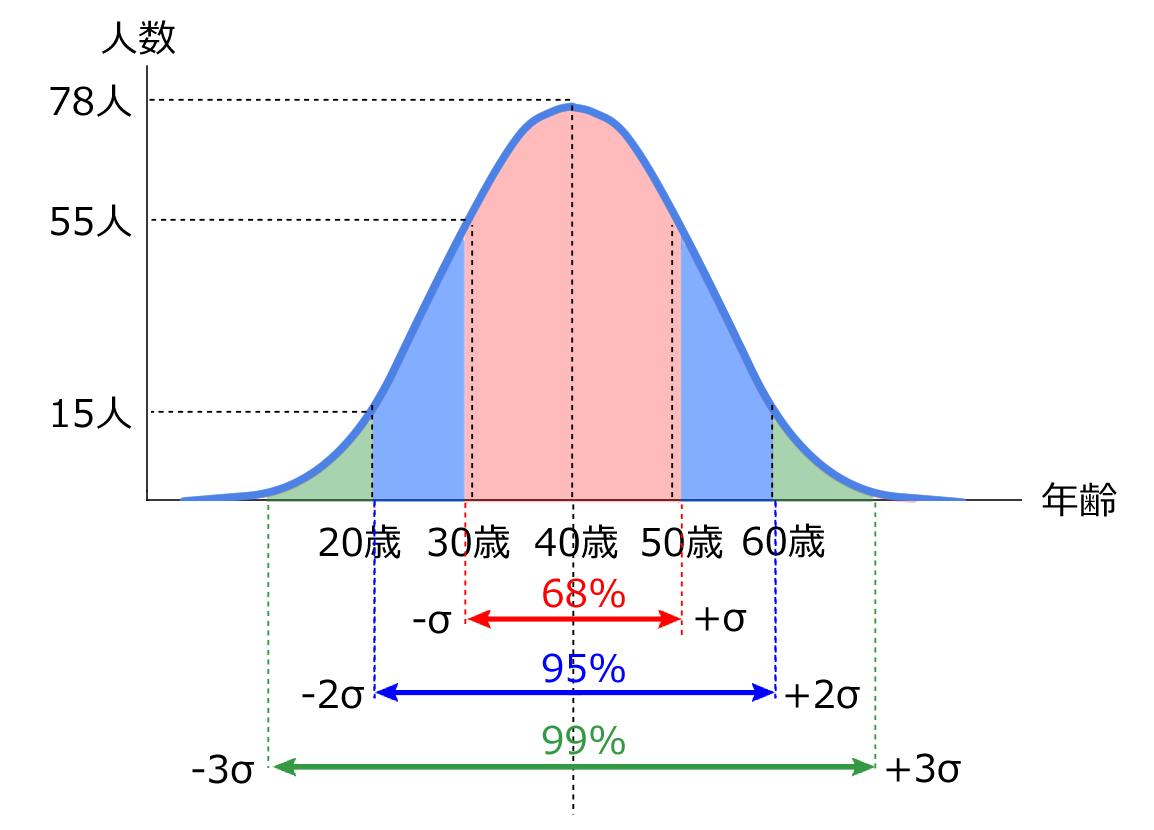
上図のデータから標準偏差を求めると、「全体の68%は29歳~51歳の中にいる」などのデータのばらつき具合を数値で表せられるようになります。
標準偏差はσという記号で表されることが多く「シグマ」と読みます。下図の例では平均が40歳なので「全体の68%は40歳-σから40歳+σの中にいる」と言い換えることができます。
まとめると、下表になります。ちなみに、ボリンジャーバンドの「ボリンジャー」はこれを開発した人の名前です。「バンド」はベルトや帯のことをいいます。
| 標準偏差 | |
|---|---|
| σ | 全体の68%は(平均-σ)から(平均+σ)の中にある |
| 2σ | 全体の95%は(平均-2σ)から(平均+2σ)の中にある |
| 3σ | 全体の99%は(平均-3σ)から(平均+3σ)の中にある |
標準偏差は以下の公式で求めることができます。以降の説明を分かりやすくするために「各データの値」という文言を「各データの価格」に変えています。この公式を使って後ほど実際に計算してみます。
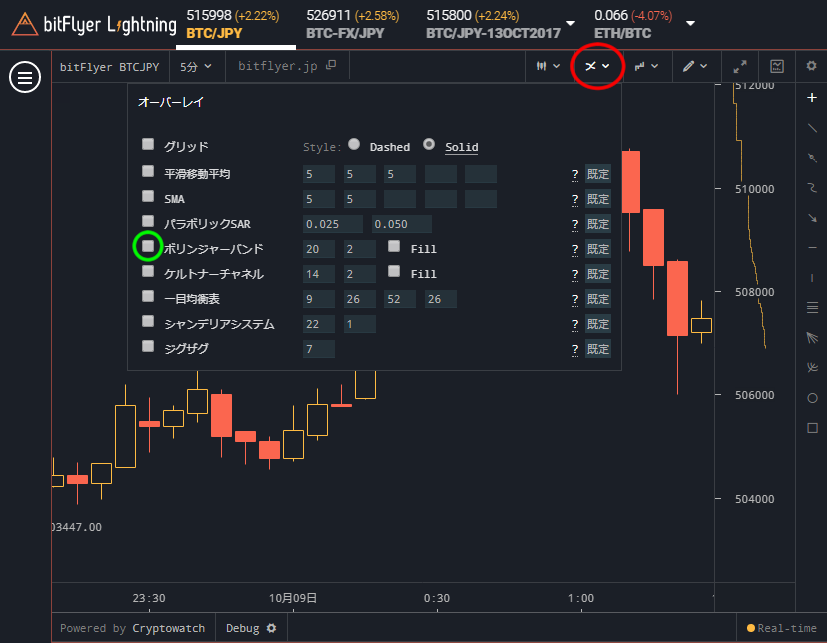
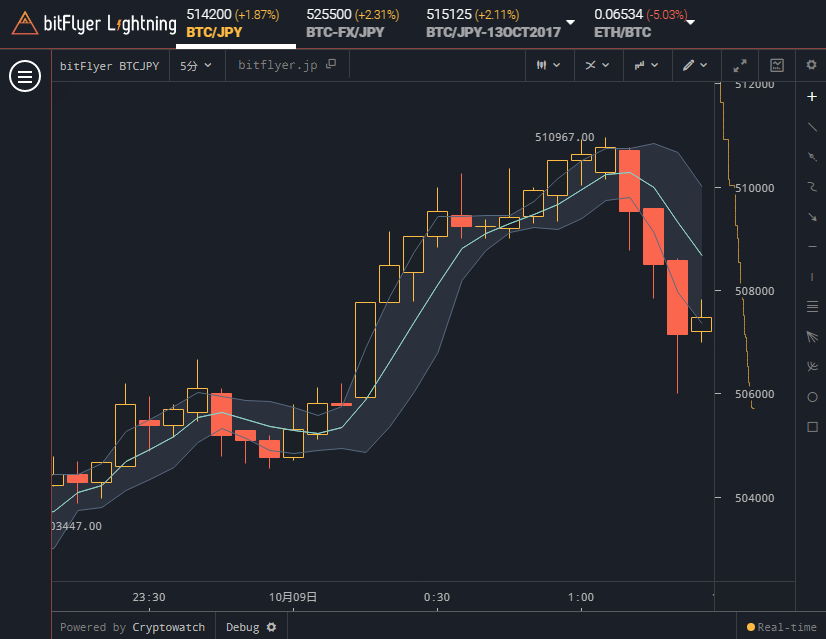
ではbitFlyer Lightningのボリンジャーバンドを表示してみましょう。下図赤枠にマウスポインタを合わせると下にオーバーレイの設定項目が表示されます。ボリンジャーバンドのチェックを入れると表示され、チャックを外すと非表示になります。
ボリンジャーバンドの隣りにある2つの入力欄は、左は移動平均線の集計範囲を設定する箇所です。右側は標準偏差に掛ける係数です。1ならσ、2なら2σになります。Fillはボリンジャーバンドの補助線に囲まれている領域を塗りつぶすかどうかの設定です。
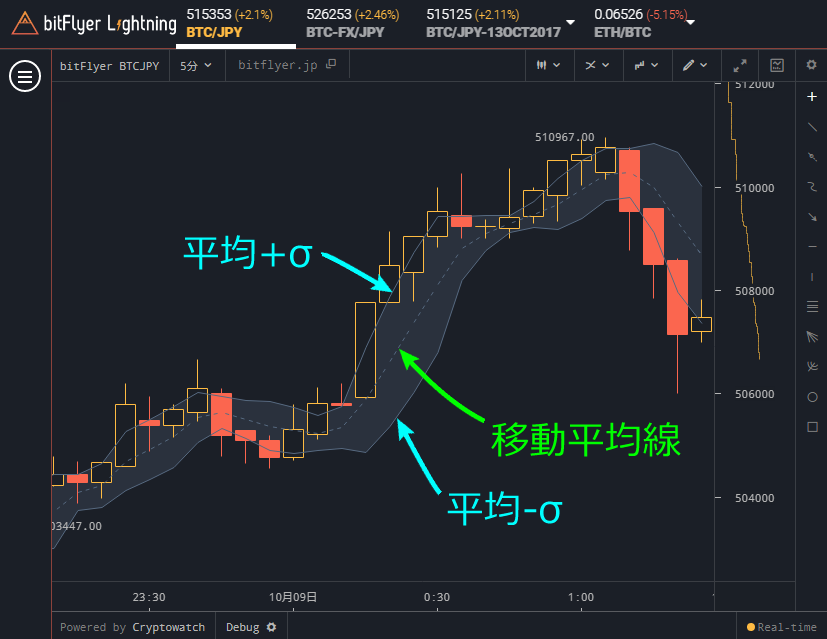
下図はボリンジャーバンドの設定を「5」、「2」、「Fillにチェック」にして表示させた結果です。
バンド(帯)っぽいものが表示されました。帯の真ん中を通っている点線は移動平均線です。移動平均線の上にある線は平均+σ、下にある線は平均-σの線です。
ボリンジャーバンドの真ん中を通っている移動平均線は単純移動平均線(SMA)です。試しにSMAの設定値を同じ5にして表示させてみたところ、下図のように線が完全に一致しました。
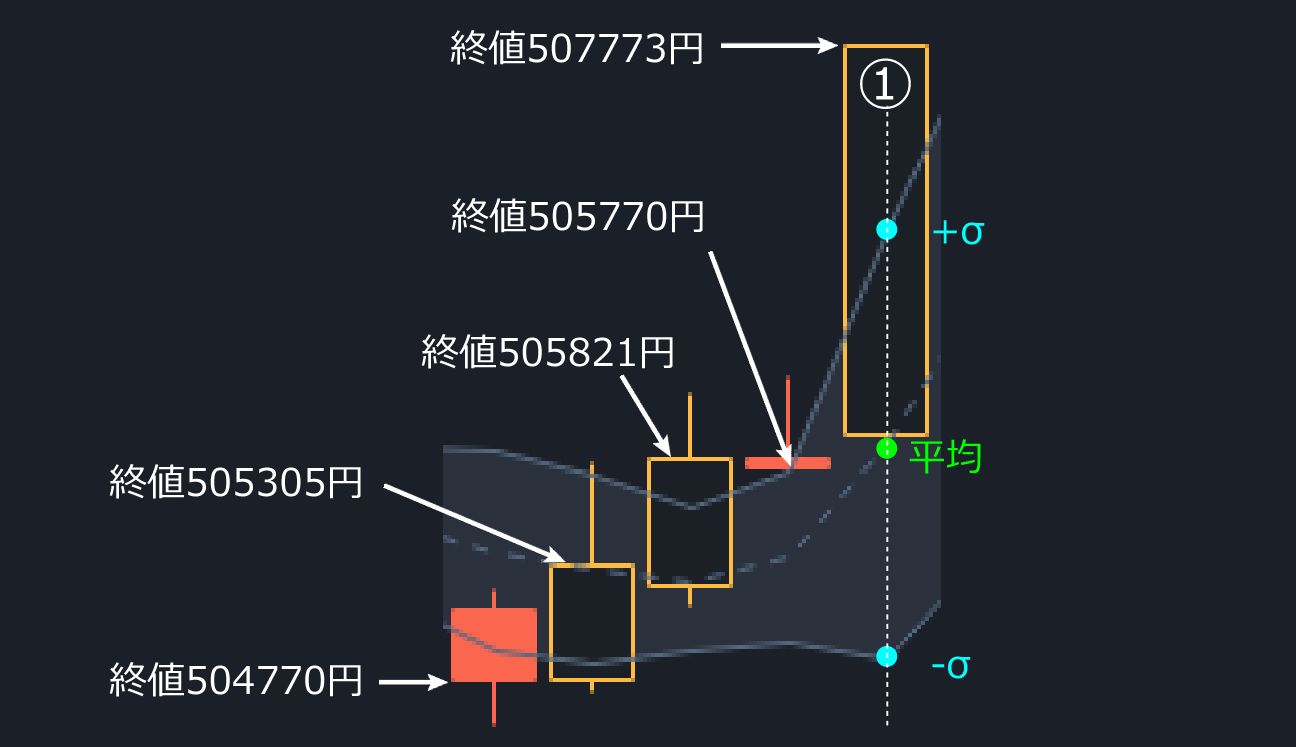
それでは、実際に標準偏差を計算してみましょう。下図はローソク足5個ぶんの終値を表示したものです。これをもとに①の場所の移動平均、標準偏差σを計算し、ボリンジャーバンドの座標と一致するかを確かめます。
まずはローソク足5個の終値の平均を求めます。
(504770 + 505305 + 505821 + 505770 + 507773) ÷ 5 = 505887
次に、標準偏差の公式に当てはめて計算した結果は以下になります(式は省略)。
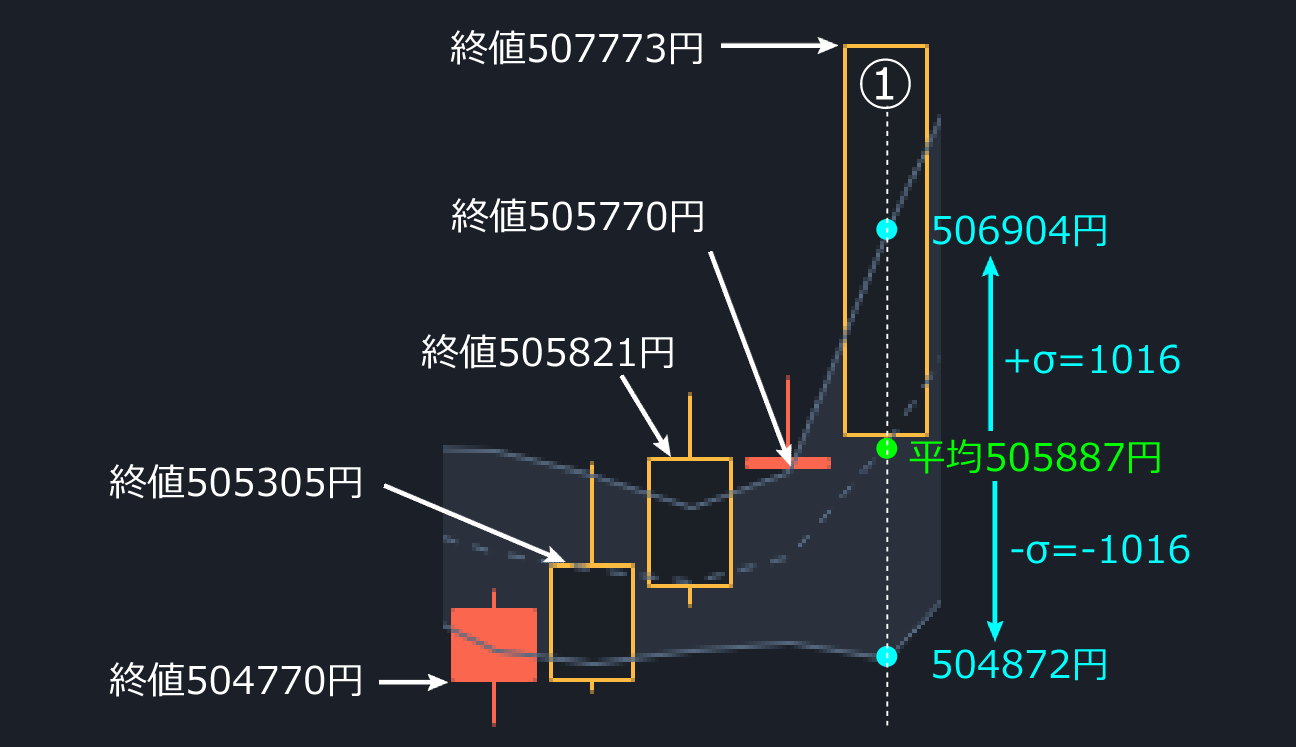
σ = 1016
移動平均線より上の線の座標は505887 + 1016 = 506904円。下の線の座標は505887 – 1016 = 504872円。ボリンジャーバンドの座標と一致しました。
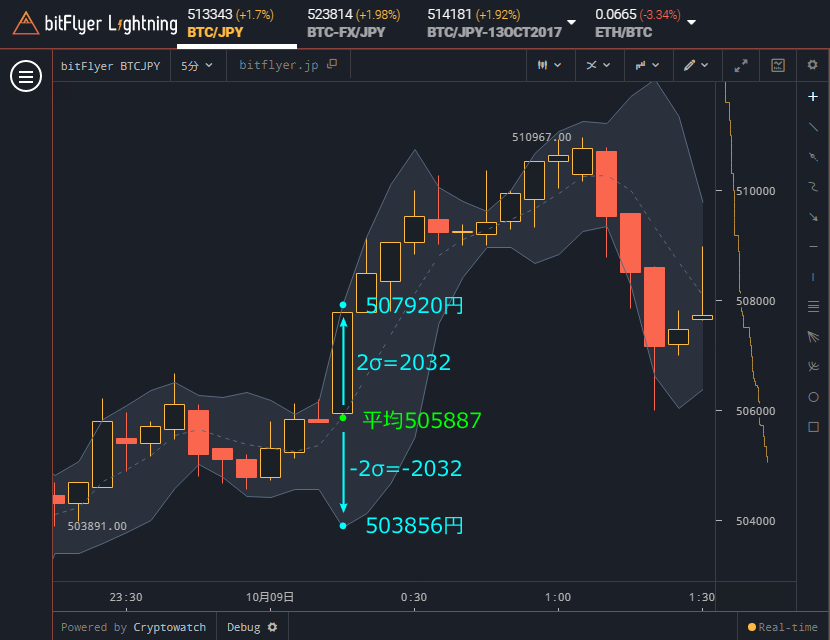
2σの線を表示するとどうなるかも確認しておきましょう。下図チャートはボリンジャーバンドの設定を2σに変更したものです。
2σ = 2 × 1016 = 2032
移動平均線より上の線の座標は505887 + 2032 = 507920円。下の線の座標は505887 – 2032 = 503856円。ボリンジャーバンドの座標と一致しました。
本記事の最初に説明したように、標準偏差はデータのバラツキ具合を表現する指標で「全体の〇%が平均±σ」の中にあることを把握するのに使えます。例えば、「全体の95%が平均±2σ」の範囲の中にあるならば、価格がその範囲を超えることは相当珍しいことであることが分かります。
価格がボリンジャーバンドの範囲を超えるのが珍しいことであるということは、範囲を超えた価格は近いうちにボリンジャーバンドの中に戻ってくる確率が高いことが分かります。
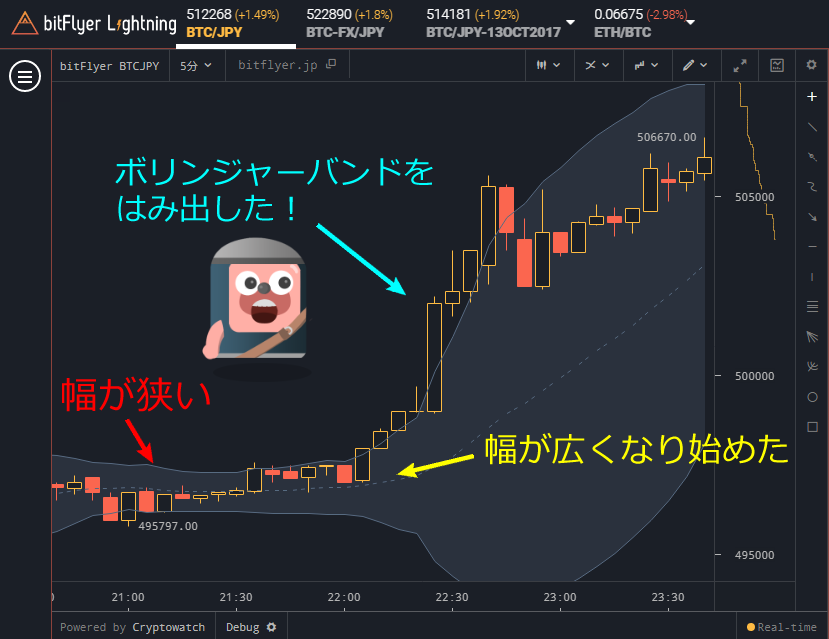
例えば、下図は2σのボリンジャーバンドですが、ローソク足がボリンジャーバンドを大きく上に突き抜けました。その後少し経ったらボリンジャーバンドの中に戻っていってます。この動きを売買タイミングに生かすのがボリンジャーバンドの使いどころです。
また、価格の動きが小さいところのボリンジャーバンドの幅は狭くなります(下図赤線)。このような状況は価格の方向はどっちつかずのことが多いので様子見を選択する人が多いです。
一方、価格が大きく動き出したらボリンジャーバンドの幅は急に広くなります。そのときローソク足がボリンジャーバンドを超えてきたら買われすぎや売られすぎによる反発に注意しましょう。大きく開いたボリンジャーバンドの上の線に沿って上昇トレンドが続いているときは、サーフィンで波に乗っているような気分になるでしょう。(・□・;)ナルノカ !?